
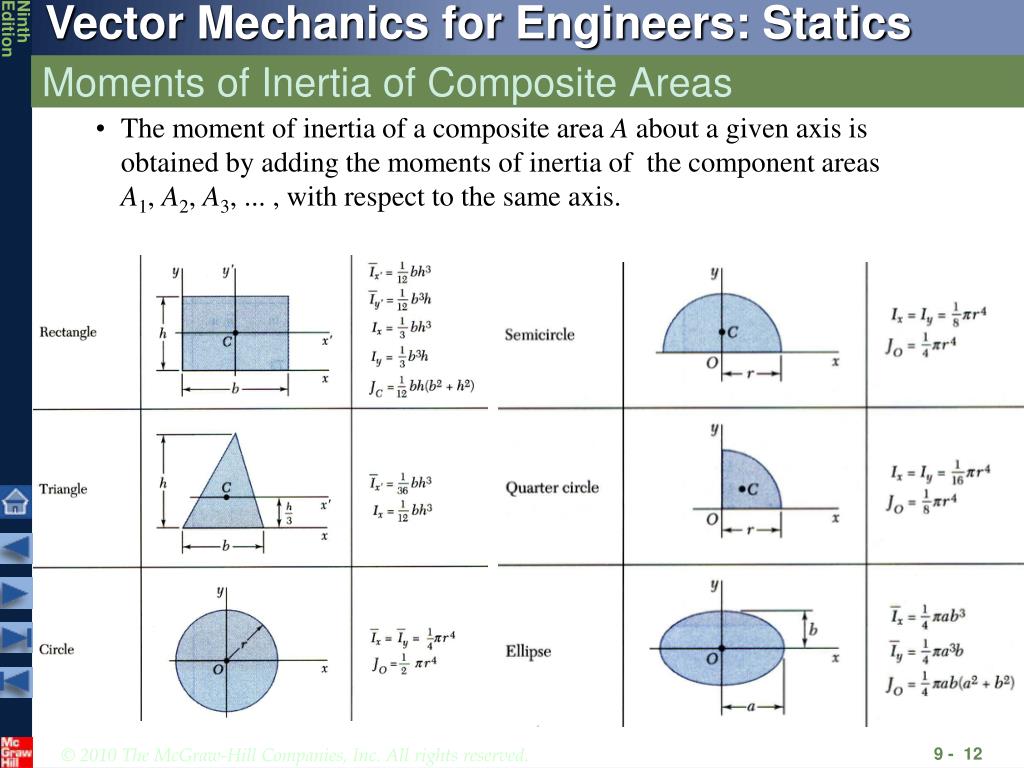
If we consider the diameter of a circle D, then we must also take ‘r’ the radius as D/2. Moment of Inertia of a Circle about its Diameter In the case of a quarter circle the expression is given as: In the case of a semi-circle the formula is expressed as: In the case of a circle, the polar moment of inertia is given as: Similarly, the moment of inertia of a circle about an axis tangent to the perimeter(circumference) is denoted as:
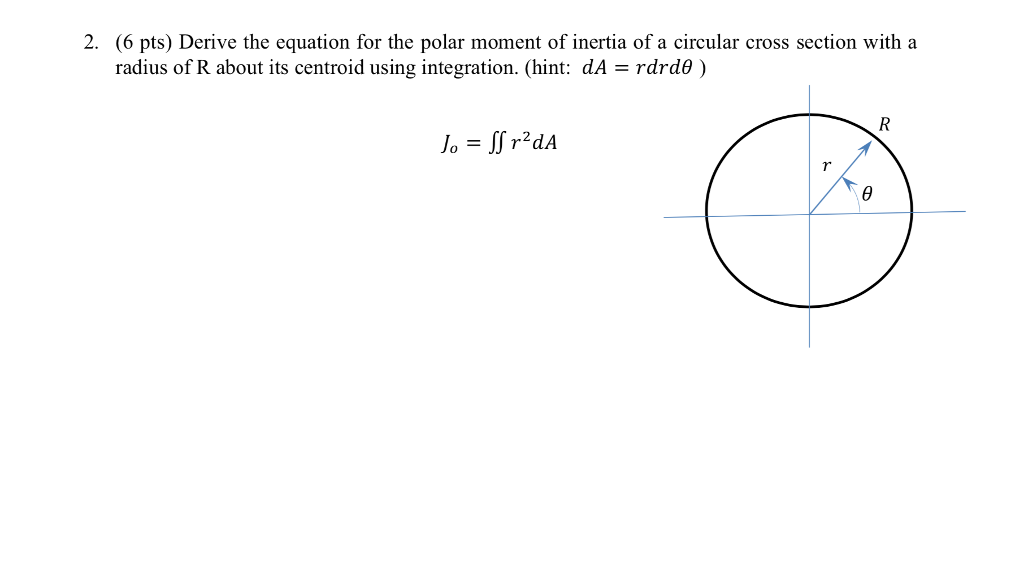
The moment of a circle area or the moment of inertia of a circle is frequently governed by applying the given equation: The moment of Inertia formula can be coined as: Mathematically, it is the sum of the product of the mass of each particle in the body with the square of its length from the axis of rotation. Yes, the proper definition of the moment of inertia is that a body tends to fight the angular acceleration. When a body starts to move in rotational motion about a constant axis, every element in the body travels in a loop with linear velocity, which signifies, every particle travels with angular acceleration. It can be inferred that inertia is related to the mass of a body.
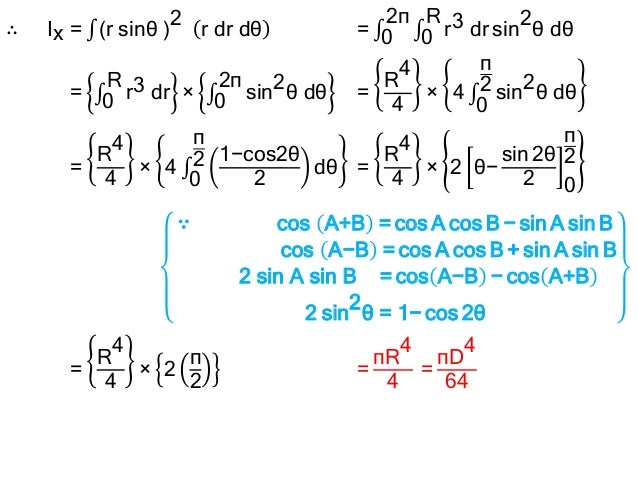
First of all, let us discuss the basic concept of moment of inertia, in simple terms.


 0 kommentar(er)
0 kommentar(er)
